Meaning of Bond and Bond Valuation
A bond is a long-term debt instrument issued by governments, public sector institutions, financial institutions or companies to raise funds from investors. When an investor buys a bond, he is actually lending money to the issuer. In return, the issuer promises to pay periodic interest (coupon) and to repay the principal (face value) at maturity.
Bond valuation means finding the fair or intrinsic value of a bond. In banking and finance, this value is calculated as the present value of all future cash flows that the bond will generate. These cash flows include:
- Periodic interest payments (coupon)
- Repayment of face value at maturity
Banks actively value bonds because they hold large investments in government securities (G-secs), corporate bonds and other fixed income instruments. Proper valuation is essential for investment decisions, treasury operations, risk management and regulatory compliance.
Cash Flows of a Bond
The cash flows of a bond are predictable and fixed, which makes bond valuation different from equity valuation.
A bond generally has:
- Face Value (FV): Amount payable at maturity (usually ₹100 or ₹1,000)
- Coupon Rate: Fixed interest rate on face value
- Coupon Payment: Interest paid periodically (annual, semi-annual, etc.)
- Maturity Period: Time after which face value is repaid
- Yield / Required Rate of Return: Market interest rate used for discounting
Example explanation:
If a bond has a face value of ₹1,000, a coupon rate of 8% and maturity of 5 years, it will pay ₹80 every year for 5 years and ₹1,000 at the end of the 5th year.
Concept of Time Value of Money in Bond Valuation
Bond valuation is based on the principle of Time Value of Money, which states that money today is worth more than money in the future. This is because money today can be invested and earn returns.
Therefore, future bond cash flows are discounted to their present value using the market yield or required rate of return.
Formula for Bond Valuation
The value of a bond is calculated as:
Bond Value = Present Value of Interest Payments + Present Value of Face Value
In formula form:
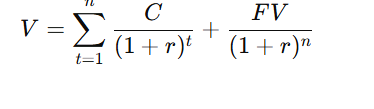
Where:
- V = Value of bond
- C = Annual coupon payment
- r = Market yield / required rate of return
- n = Number of years to maturity
- FV = Face value
Conceptual clarity is more important than complex calculation.
Relationship between Coupon Rate, Yield and Bond Value
This is one of the most important areas for JAIIB / CAIIB exams.
When Coupon Rate = Yield
If the coupon rate of a bond is equal to the market yield, the bond will sell at par, meaning its value will be equal to its face value.
When Coupon Rate > Yield
If the coupon rate is higher than the market yield, the bond becomes more attractive. Investors are willing to pay more than face value. In this case, the bond sells at a premium.
When Coupon Rate < Yield
If the coupon rate is lower than the market yield, the bond is less attractive. Investors pay less than face value. In this case, the bond sells at a discount.
Bond Price and Interest Rate Relationship
Bond prices and interest rates have an inverse relationship. This is a fundamental concept tested repeatedly in banking exams.
When market interest rates rise:
- Existing bonds with lower coupon rates become less attractive
- Bond prices fall
When market interest rates fall:
- Existing bonds with higher coupon rates become more attractive
- Bond prices rise
This inverse relationship exists because bond cash flows are fixed, while discount rates change.
Bond Valuation Theorems (Very Important for Exams)
Bond valuation theorems explain how bond prices behave when interest rates, maturity and coupon rates change.
Theorem 1: Inverse Relationship between Bond Price and Yield
Statement:
Bond prices move inversely with market yields.
Explanation:
When the required rate of return increases, future cash flows are discounted at a higher rate, reducing the present value of the bond. Similarly, when yield decreases, the present value increases.
Exam Focus:
This theorem explains interest rate risk faced by banks holding long-term bonds.
Theorem 2: Bond Price Sensitivity Increases with Maturity
Statement:
For a given change in yield, the price of a long-term bond changes more than that of a short-term bond.
Explanation:
Long-term bonds have cash flows spread over a longer period. Therefore, a change in discount rate affects more cash flows, leading to higher price volatility.
Banking relevance:
Banks prefer shorter-duration securities when interest rate volatility is high.
Theorem 3: Lower Coupon Bonds Are More Sensitive to Yield Changes
Statement:
For a given maturity, bonds with lower coupon rates are more sensitive to changes in interest rates.
Explanation:
Low-coupon bonds receive most of their value at maturity. Hence, changes in discount rate have a greater impact on present value.
Theorem 4: Price Increase from Yield Decrease is Greater than Price Decrease from Yield Increase
Statement:
For a given bond, the percentage increase in price due to a fall in yield is greater than the percentage decrease in price due to a rise in yield of the same magnitude.
Explanation:
This phenomenon is due to convexity of bond prices. Bond price-yield relationship is not a straight line but a curved one.
Theorem 5: Premium and Discount Bonds Move Towards Par Value
Statement:
As a bond approaches maturity:
- Premium bonds decline in value
- Discount bonds increase in value
- Both move towards par value
Explanation:
At maturity, all bonds are redeemed at face value regardless of their market price earlier.
Yield Measures Used in Bond Valuation
Banks use different yield measures to evaluate bonds.
Current Yield
Current yield is calculated as: Current Yield= Market Price/ Annual Coupon
It ignores capital gain or loss and time value of money. Hence, it is not a complete measure.
Yield to Maturity (YTM)
Yield to Maturity is the most important yield measure in banking exams.
YTM is the discount rate at which the present value of all future cash flows equals the market price of the bond. It considers:
- Coupon income
- Capital gain or loss
- Time value of money
Banks use YTM to compare bonds with different coupons and maturities.
Importance of Bond Valuation in Banking
Bond valuation plays a crucial role in banking operations.
- Banks invest heavily in government securities to meet SLR requirements
- Treasury departments manage interest rate risk
- Valuation affects profit and loss account
- Mark-to-market valuation impacts capital adequacy
- RBI monetary policy directly influences bond prices
Key Points to Remember
- Bond value is the present value of future cash flows
- Bond prices and interest rates move inversely
- Long-term bonds are more risky than short-term bonds
- Low coupon bonds are more sensitive to yield changes
- All bonds converge to face value at maturity
- YTM is the most comprehensive yield measure
Conclusion
Bond valuation is a core concept in banking and finance, especially for treasury and investment functions. Understanding the logic behind valuation and theorems is more important than memorizing formulas. A clear grasp of how interest rates affect bond prices helps bankers manage risk, profitability and regulatory requirements effectively.
